简单的一种解释是：在完全二叉树中，低层元素的数量要远远少于高层的数量。高层元素的高度较高而深度较低；底层元素的高度较低而深度较高。由于上滤操作的时间复杂度正比于高度，对于存在大量底层元素的完全二叉堆很不友好，使得基于上滤的批量建堆算法效率较低。

   
     * 批量建堆（将内部数组转换为完全二叉堆）
     *  heapify(){
         获取下标最大的 内部非叶子节点
        int lastInternalIndex = getLastInternal();

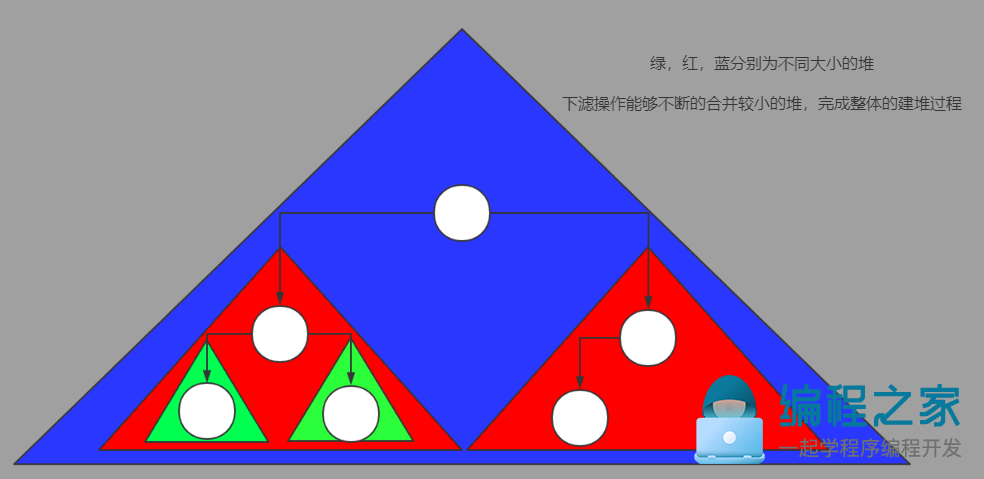
         Floyd建堆算法 时间复杂度"O(n)"
         从lastInternalIndex开始向前遍历，对每一个元素进行下滤操作，从小到大依次合并
        for(int i=lastInternalIndex; i>=0; i--){
            siftDown(i);
        }
    }

4.堆排序

堆排序主要分为两步进行：

　　1.?堆排序首先将传入的数组转化为一个堆(floyd建堆算法，时间复杂度O(n))。

　　2.?和选择排序类似，堆排序每次都从未排序的区间中选择出一个极值元素置入已排序区域，在堆中极值元素就是堆顶元素，可以通过popMax方法(时间复杂度O(logN))获得。从数组末尾向前遍历，循环往复直至排序完成，总的时间复杂度为O(N logN)。

　　综上所述，堆排序的渐进时间复杂度为O(N?logN)。同时由于堆排序能够在待排序数组中就地的进行排序，因此空间效率很高，空间复杂度为(O(1))。

 static <T>  heapSort(T[] array){
        CompleteBinaryHeap<T> completeBinaryHeap = new CompleteBinaryHeap<>(array);

        int i=array.length-1; i>=0; i--){
            array[i] = completeBinaryHeap.popMax();
        }
    }

5.完整代码

优先级队列ADT接口：

 1 /**
 2  * 优先级队列 ADT接口
 3   4 {
 5 
 6      7      * 插入新数据
 8      *  newData 新数据
 9      * 10      insert(E newData);
11 
12     13      * 获得优先级最大值（窥视）
14   当前优先级最大的数据
15 16     E peekMax();
17 
18     19      * 获得并且删除当前优先级最大值
20   被删除的 当前优先级最大的数据
21      22     E popMax();
23 
24     25      * 获得当前优先级队列 元素个数
26  当前优先级队列 元素个数
27 28      size();
29 
30     31      * 是否为空
32  true 队列为空
33      *          false 队列不为空
34 35      isEmpty();
36 }

完全二叉堆实现:

 * 完全二叉堆 实现优先级队列
  =========================================成员属性===========================================
     size;

     ===========================================构造函数========================================
     ==========================================外部方法===========================================

    @Override
            siftUp(lastIndex);
    }

    @Override
     E peekMax() {
         内部数组第0位 即为堆顶max
        this.innerArrayList.get(0);
    }

    @Override
     max;
    }

    @Override
     size() {
        .size;
    }

    @Override
     isEmpty() {
        this.size() == 0;
    }

    @Override
     String toString() {
        :::空列表
        .isEmpty()){
            return "[]";
        }

        :::列表起始使用"["
        StringBuilder s = new StringBuilder("[":::从第一个到倒数第二个元素之间
        int i=0; i<size-1; i++:::使用","进行分割
            s.append(this.innerArrayList.get(i)).append(",").append(" ":::最后一个元素使用"]"结尾
        s.append(this.innerArrayList.get(size-1)).append("]");
         s.toString();
    }

     completeBinaryHeap.popMax();
        }
    }

     =========================================内部辅助函数===========================================
    ;
            }
        }
    }

     leftIndex;
                }
            }
        }
    }

    ){
            siftDown(i);
        }
    }

    
     * 获得当前向量末尾下标
     * 

　　本系列博客的代码在我的 github上：https://github.com/1399852153/DataStructures?，存在许多不足之处，请多多指教。

（编辑：ASP站长网）